El **teorema de Cardano**, desarrollado por Gerolamo Cardano en el siglo XVI, se refiere a un método para resolver ecuaciones cúbicas. Cardano describió su método en su obra *Ars Magna*, publicada en 1545. Aunque él popularizó el método, las ideas fundamentales fueron previamente desarrolladas por matemáticos como Niccolò Tartaglia y Scipione del Ferro.
### Fundamentación Teórica
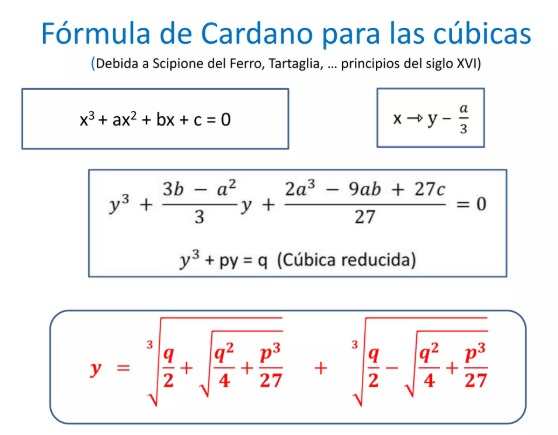
1. **Ecuación Cúbica**: La forma general de una ecuación cúbica es \( Ax^3 + Bx^2 + Cx + D = 0 \), donde \( A \neq 0 \) y \( A, B, C, D \) son coeficientes. Para aplicar el método de Cardano, es común transformar la ecuación en su forma reducida, que es \( z^3 + pz + q = 0 \). Esto se logra eliminando el término cuadrático mediante un cambio de variable adecuado[^1](https://www.esfm.ipn.mx/assets/files/esfm/docs/RNAFM/articulos-2022/XXVIIRNAFM044.pdf).
2. **Transformaciones**: Se define \( z = x + \frac{B}{3A} \) para facilitar la resolución. Esto transforma la ecuación cúbica a una forma más manejable, utilizando los nuevos parámetros \( p \) y \( q \) que dependen de los coeficientes originales[^3](https://www.scribd.com/document/684813603/Metodo-de-Cardano-TEO).
3. **Solución**: La solución se basa en encontrar dos números \( u \) y \( v \) tales que \( u^3 + v^3 = -q \) y \( uv = -\frac{p}{3} \). De aquí, las raíces de la ecuación se pueden determinar a través de:
\[
z = u + v
\]
donde \( u \) y \( v \) son calculados a partir de las ecuaciones anteriores[^1](https://www.esfm.ipn.mx/assets/files/esfm/docs/RNAFM/articulos-2022/XXVIIRNAFM044.pdf).
4. **Discriminante**: El discriminante de la cúbica, el cual se denota como \( \Delta = \frac{q^2}{4} + \frac{p^3}{27} \), ayuda a determinar la naturaleza de las raíces:
- \( \Delta > 0 \): La ecuación tiene una raíz real y dos complejas.
- \( \Delta = 0 \): Todas las raíces son reales y al menos dos son iguales.
- \( \Delta < 0 \): Todas las raíces son reales y distintas[^5](https://es.wikipedia.org/wiki/Ecuaci%C3%B3n_de_tercer_grado).
### Ejemplo de Aplicación
Si tenemos una ecuación cúbica como \( x^3 + 3x + 1 = 0 \):
1. Se identifica \( p = 3 \) y \( q = 1 \).
2. Se encuentra el discriminante:
\[
\Delta = \frac{1^2}{4} + \frac{3^3}{27} = \frac{1}{4} + 1 = \frac{5}{4} > 0
\]
Esto indica que hay una raíz real y dos complejas.
3. Aplicando el método de Cardano, se calculan las raíces utilizando las fórmulas descritas anteriormente.
### Contexto Histórico
El desarrollo del teorema de Cardano estuvo envuelto en controversias. Tartaglia le reveló sus métodos bajo condiciones de confidencialidad, pero Cardano, al conocer el trabajo previo de Scipione del Ferro, publicó los resultados sin tener en cuenta las promesas hechas a Tartaglia[^2](https://es.slideshare.net/slideshow/ecuaciones-de-tercer-grado-37897888/37897888). Esto llevó a un conflicto histórico entre ambos matemáticos.
El uso de este método sigue siendo relevante en la teoría de ecuaciones y análisis algebraico, a pesar de ser considerado laborioso en comparación con métodos numéricos modernos. Sin embargo, marcó un punto crucial en la historia de las matemáticas, al abrir la puerta al uso de números complejos y al desarrollo posterior de la teoría de ecuaciones más complejas[^3](https://www.scribd.com/document/684813603/Metodo-de-Cardano-TEO).
### Conclusión
El teorema de Cardano no solo es un hito en la resolución de ecuaciones cúbicas, sino que también es esencial en la historia de las matemáticas, marcando la transición hacia la utilización de números complejos y estableciendo un puente hacia métodos más avanzados que se emplearían en siglos posteriores.

























Comentarios
Publicar un comentario